三维音频距离感知敏感度的测量与分析

2022-06-20 17:56:28

---

摘要：

虚拟现实与多媒体技术的快速发展使三维音频的应用增多。传统的三维音频感知测量主要集中在人耳对方位感知性能上，欠缺对距离感知性能的深入研究，现有的三维音频感知特性的研究不足以支撑三维音频在距离感知性能方面的提升。通过三维音频距离感知敏感度的实验，得到距离、角度等因素对距离感知敏感度变化的影响规律，以及不同距离时的距离感知阈值。

引言

传统的三维音频可以分为多声道三维音频和双耳三维音频。多声道三维音频主要通过扬声器的排列呈现三维音频的效果，而双耳三维音频则是通过头相关传递函数（HRTF，Head Related Transfer Functions ）实现的，它利用原始音频与其时域对应的头相关冲激响应（HRIR，Head-Related Impulse Response）进行卷积，从而得到包含声源与听音者间方位角、高度角和距离的双耳三维音频信号，其对硬件需求较小，方便携带。但是，由于人耳对距离感知是由强度、混响、频谱及双耳间差异等复杂因素共同决定的，所以仅通过HRIR无法合成距离信息准确的双耳三维音频。因此，探究人耳对三维音频的距离感知特性，尤其是实际声场环境下的表现，对于提升三维音频空间听觉效果的研究及其应用具有参考价值。

近年来，一些学者提出了基于距离的三维音频恢复和编码的方法。2014年，Zahorik P等人结合混响与幅度调制技术，提高了在混响环境中，单声道音频的距离感知效果[4]。2016年，Spagnol S等人提出了近场声像滤波器模型，通过使用延迟回馈滤波器组实现距离恢复函数模型[5]。2017年，Koutny等人提出了利用球谐函数分解的声源距离恢复算法，该算法主要用于多通道三维音频系统中的双耳三维音频恢复。2019年，李念等人研究了听觉距离线索感知特性和定位机理及其在3D音频编码中的应用。

传统的三维音频感知特性的研究主要针对水平角和高度角，但随着基于距离的音频重建和编码的提出，部分学者也展开了对三维音频距离的感知特性的研究。2016年，法国布雷斯特大学的Mathieu Paquier等人开展了听觉、视觉对距离感知影响的联合研究。2017年，武汉大学杨乘等人对三维空间距离感知特性进行了研究。

综上所述，一方面实际应用中对三维音频空间距离感知性能的要求提高，另一方面传统的三维音频感知特性的研究主要集中在水平面和垂直面，对三维空间内距离感知特性的研究较少，相关实验主要是通过在消音室中不同位置的声音进行采集后，受试者利用耳机进行测听，zui终得到三维音频的感知特性，鲜有在实际的声场环境下进行测量。传统的实验环境虽然可以满足对不同方位感知敏感度的测量，但是削弱了对距离的感知。针对上述存在的问题，笔者在三维音频感知特性的实验基础上，充分考虑其他因素对距离感知特性的影响，设计了三维音频距离感知特性的实验，采用受试者现场测听，通过改变距离、角度得到相关数据，并进行统计分析得到三维音频距离感知敏感度的变化情况和不同距离的距离感知阈值。

1、距离感知敏感度的测量

由于环境和人体自身的生理结构等因素的影响，人耳对音频方位的变化存在一定的感知阈值，只有当空间方位的变化达到一定阈值时，人才能感受到方位的变化，这种感知阈值被称为恰感知差异（JND，Just Notice Difference）。距离感知敏感度（DPS，Distance Perception Sensitivity）是指人耳对音频在距离变化的感知特性。

1.1 实验环境配置

传统的感知敏感度实验主要围绕角度的变化进行测试，测试主要通过采集消音室中不同角度的声音，通过耳机进行角度辨别，zui终得到感知敏感度。但是，这种传统测试方式得到的DPS会受到一些因素的影响，首先，受试者在使用耳机进行测听实验时，往往会因为头中定位（IHL，Inside-the-head Localization）的影响，感觉声像主要集中在人头内部，不能很好地感知距离的变化；其次，根据研究，在混响情况下，人耳对声源方向的定位能力不如在消音室中，相反，人耳对声源距离的定位能力在混响情况下比消音室里更准确。综上所述，本实验安排在长6.2 m、宽3.4 m、高2.8 m的听音实验室中进行，该房间经过吸声处理，室内环境噪声不大于40 dB，混响时间约为0.4 s，该混响时间既可以满足听音室的混响时间要求，又更加接近日常室内环境的混响时间。

对于研究不同距离DPS的实验，把扬声器固定在一个标有刻度且可以前后移动的支架上，支架高度为使扬声器与人耳处在同一高度，通过控制移动扬声器控制声源到人耳的距离。对不同水平角度的DPS进行测量的实验，采用旋转座椅来调整角度，如图1所示。

图1 距离感知敏感度测试示例

实验使用的扬声器为JBL Control 12C-VA吸顶扬声器，该扬声器的净尺寸为3 in（7.6 cm），频响范围在68 Hz～17 kHz。该扬声器方便固定和移动，同时由于其尺寸较小，可以更好地满足本次测试的需求。考虑到扬声器移动过程中产生的噪声影响测试结果，支架使用了静音轨道，其在移动过程中产生的轻微噪声可以忽略不计。

由于高斯白噪声没有严格的周期性，可以有效地减少相位混淆现象的发生，同时高斯白噪声包含全频带的频率成分，所以本次实验使用高斯白噪声作为主观听音测试的音频信号，由Audition生成，时为长600 ms，采样率48 kHz、精度16 bit单声道，zui高频率为20 kHz，zui低频率为20 Hz。

参与本实验的有8名测试人员，其中5名男性，3名女性，年龄在20～25岁之间，都有主观三维音频的相关听音实践经验。在测听实验之前，受试者需要进行三维音频距离感知的听音训练，使其可以更好地判断远近。在听音训练结束后，受试者需要完成参考音为100 cm，测试音为125 cm的固定点的听音测试，测试过程中参考音和测试音会随机播放，共40次，测试人员需要在2 s内判断声音远近变化，zui终只有当正确率超过80%才可以参与正式的测听实验。考虑到受试者需要对136个测试点进行测听，每个测试点可能需要测听30次以上，所以在测试前会告知受试者本次测听的具体步骤，同时在每个测试点测听结束后，会让受试者休息5 min，以提高受试者的测听效率和测试结果的准确性。

1.2 实验方法

实验采用经典心理声学中1up/2down的心理测试方法[9]，该方法包含了多轮测试，每一轮测试的测试信号都依赖于前一轮的测试结果。1up/2down的意思为：当受试者连续两次判断正确时，系统在当前测试值的基础上，减小参考音与测试音之间的步长；如受试者判断错误，则将增大参考音与测试音之间的步长，生成新的测试值。记每一次步长变化为一次反转（n）。

根据前期的预实验结果，实验将变化步长（Sn）的初始值设为50 cm，步长变换次数记为n，实验过程中步长（Sn）变化公式：

对于步长变化时存在的小数部分四舍五入，以保证实验过程中步长变化的zui小值为1 cm。

根 据 初 始 步 长 和 步 长 变 换 公 式 ， 模 拟 使用1up/2down心理测试方法测试，当参考音为50 cm时步长的变化情况，如图2所示。可以看到，测试音的初始值从100 cm降到接近参考音50 cm时，需要经过13次反转。从第5次反转之后，测试值接近平稳。所以，在本次实验过程中将反转次数设为13次，对zui后五次的步长变化后的测试距离求平均值，得到某一位置的DPS。

 

图2 50 cm时测试音的变化情况示意图

实验测量了声源距离到人耳50 cm、65 cm、80 cm、100 cm、120 cm、140 cm、160 cm、180 cm、200 cm、225 cm、250 cm、275 cm、300 cm、340 cm、380 cm、420 cm、465 cm，共17个距离的数据；对应每个距离的测量垂直角均为0°，水平角如图3所示，为0°、15°、30°、45°、75°、90°、135°、180°的DPS，每个实验人员共需要进行136组听音测试。

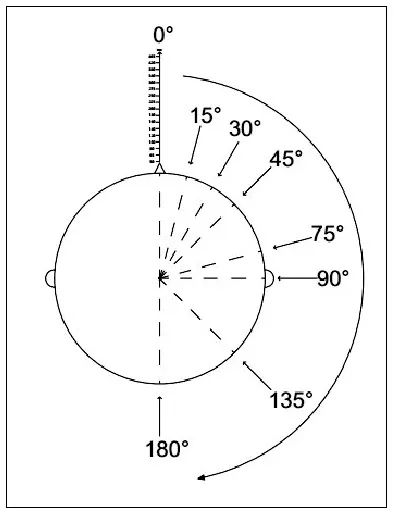
图3 实验测量范围示意图

1.3 实验步骤

本实验具体流程，如图4所示。

图4 实验流程图

步骤一：根据需要测听的水平角和距离，确定固定测听点作为参考音，选取水平角相同，距离相差一个初始步长的音频信号作为测试音。

步骤二：随机播放参考音与测试音。两段测试信号的长度均为600 ms，两段信号间的移动的时间间隔控制在1 s内。

步骤三：受试者需在2 s内做出选择，判断步骤二中播放的音频信号的位置变化情况，即判断第二个音频信号离前一个音频信号更近或更远。测试人员做出选择后无法更改，直接执行下一步骤。

步骤四：当连续两次判断正确时，将减小距离步长；为了保证实验的准确性，实验允许无法判断的情况出现，当连续出现两次无法判断的情况时，则按判断错误处理，增大距离步长；进入步骤五。

步骤五：根据白噪声的特性，长时间的测听实验可能会造成受试者产生疲劳，影响测试结果。所以，当实验测试测试次数大于40次，记该位置的DPS为0，并退出本次测试；实验测试次数小于40次，同时反转次数大于13次，则取zui后五次的测试值的平均值为该位置的DPS，否则返回步骤二继续进行测听。

2 距离感知敏感度的分析

2.1 异常值处理

受试者在测听过程中可能会出现对某一位置的声音信号无法准确定位的情况。也就是，当受试者经过40次测听，同时翻转次数小于13次的情况时，则将该点的DPS记为0。本次实验中共有三组数据出现这种情况。插值法是离散函数逼近常用的一种方法，通过插值方法可以构造连续曲面经过的全部离散点，同时根据有限个已知点的值推导未知点的值。本实验利用多项式插值法对这些数据进行替换。

多项式插值法[12]以表示某条 线段的前一个端点，表示该线段的后一个端点，则对于在范围内的横坐标为x的点，其高度y为：

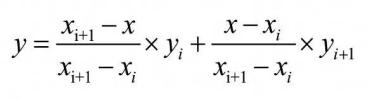
其中，yi和yi+1的两个参数称为基函数，二者之和为1，分别代表yi和yi+1对插值点高度的权值。

2.2 DPS与距离、角度的关系

不同角度时 D P S 随距离的变化如图 5 所示，在50～160 cm时，距离感知敏感度的变化较为缓慢；在160～465 cm时，距离感知敏感度的变化较为明显。在测量距离相同的情况下，不同角度的DPS的变化趋势大致相同。

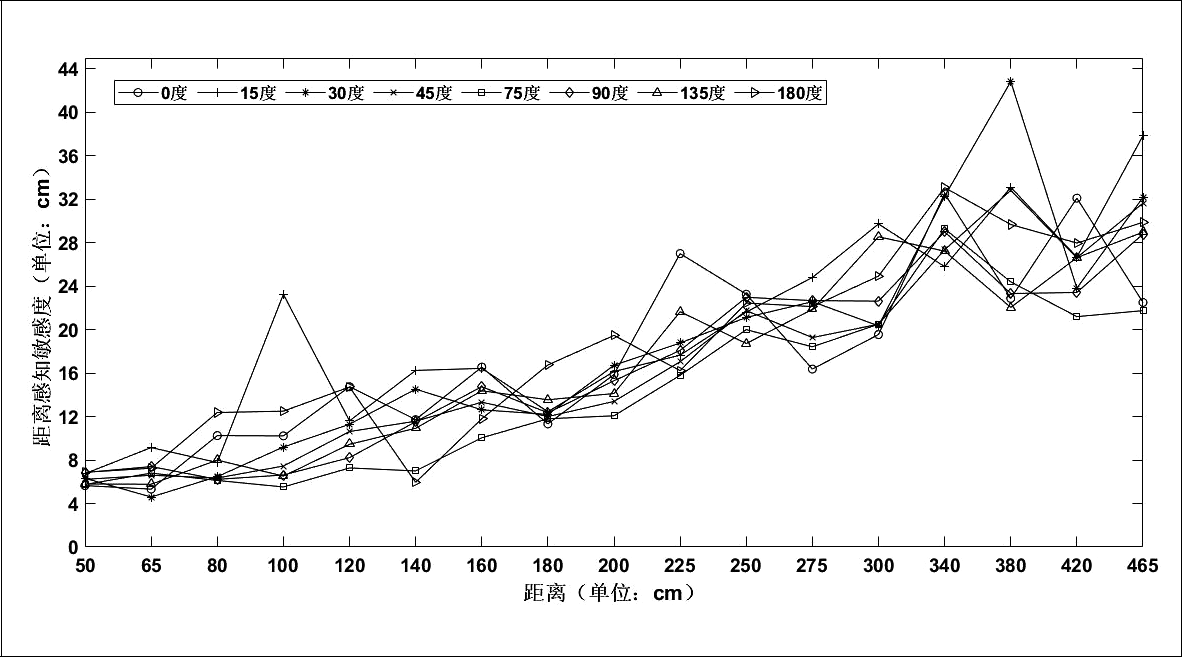
图5 不同角度时DPS随距离的变化情况

不同距离 D P S 随角度的变化如图 6 所示，在45°～75°时，不同距离的DPS都有一个明显的下降，即在这一区间内，人耳对距离的变化更为敏感；测量角度为0°和180°时，在距离相同的情况下，DPS基本一致。

图6 不同距离时DPS随角度的变化情况

为了研究整个测量范围内DPS的变化情况，在已有的实验数据基础上，采用三次样条插值的方法对测量范围内数据进行拟合。三次样条插值是通过构造分段多项式进行插值，从而可实现较小的插值误差[13]，其定义为：

设在区间[a,b]上给定一个分割

如果定义在[a,b]上的一个函数S(x)满足下列条件：

（1）在每个小区上，S(x)是三次多项式；

（2）在整个区间[a,b]上，S(x)为二阶连续可导函数，也就是说在每个节点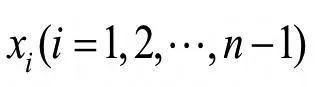处

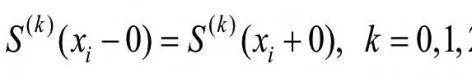
则称S(x)为三次样条插值函数。

通过对实验范围内各点进行插值拟合，zui终得到了距离感知敏感度的曲面图，如图7所示。随着距离的增大DPS的整体变化呈现增大趋势，即随着距离的增大，人对声源距离的感知减小。在60°～90°区间内，DPS出现下降，即人对声源距离变化的感知在左右两侧更为明显，这与2017年武汉大学杨乘等人对不同DPS测量数据拟合得到的DPS变化趋势基本一致。

图7 测量范围内距离感知敏感度曲面图

传统的实验仅仅对DPS的变化趋势进行分析，为了进一步研究距离和角度对DPS的影响，实验对现有数据进行多元线性回归分析，其具体数学模型如下：

假设某一因变量y受k个自变量的影响，其中n组观测值为。那么，多元线性回归模型的结构形式为：

式中，为待定参数，为随机变量。

通过对现有的实验数据进行分析，得到角度（x1）和距离（x2）对DPS的影响。如图8所示，图中P-val的值表示样本间差异由抽样误差所致的概率，当P-val<0.05为显著，P-val<0.01为非常显著，可以看到x1=0.00，x2=0.95，由此可以得到距离是DPS的主要影响因素。

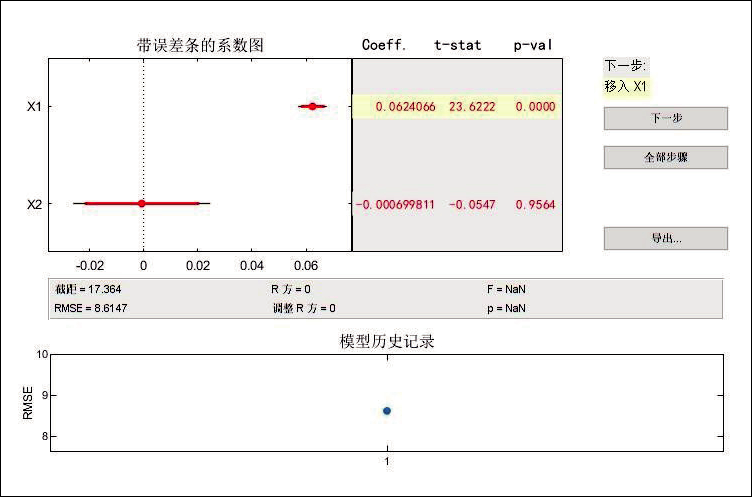
图8 距离和角度对DPS的影响

2.3 距离感知阈值

距离感知阈值（ D P T ， D i s t a n c e P e r c e p t i o n Threshold）是指当距离的变化达到一定阈值时，人才能感受到距离的变化。通过对本实验数据的分析得到100 cm、200 cm、300 cm的距离条件下的DPT，方便进行下一步的研究。上文已经对影响DPS的因素进行了分析，得到角度不是影响DPS的主要因素，所以在研究DPT时，排除角度的因素。

通过对相同距离的DPS统计，得到了测量距离为100 cm、200 cm和300 cm的DPT的分布情况，如图9、图10、图11所示。从统计结果中发现，当测量距离为100 cm和200 cm时，DPT较为集中，测量距离为300 cm时DPT分布的较为分散，和上文得到DPS随距离变化的结论一致。

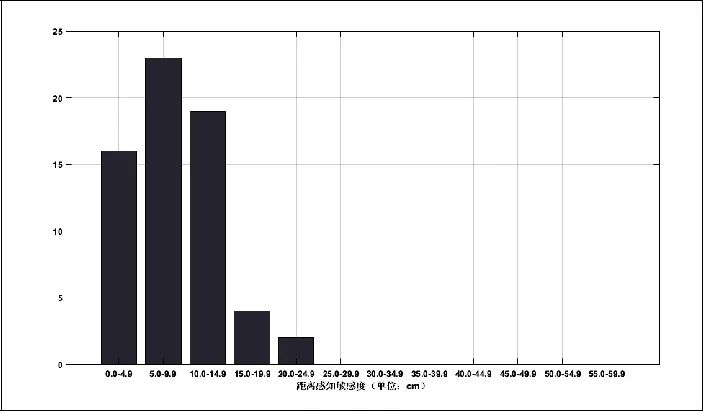
图9 测量距离100 cm 距离感知阈值的分布情况

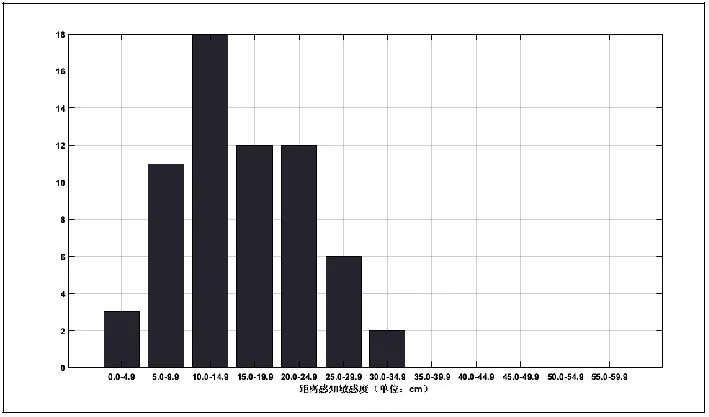
图10 测量距离200 cm 距离感知阈值的分布情况

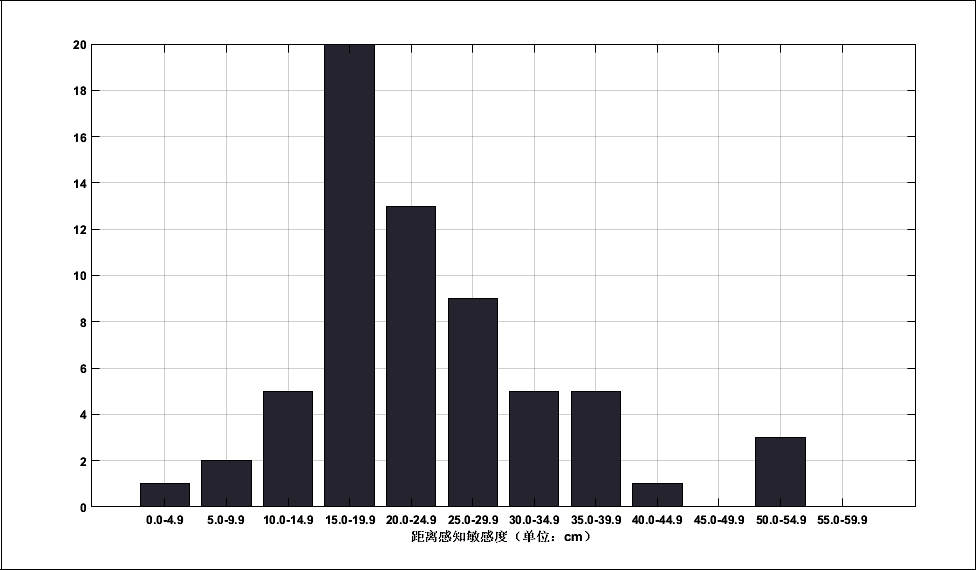
图11 测量距离300 cm 距离感知阈值的分布情况

标准偏差用来描述各数据偏离平均数的距离（离均差）的平均数。标准差能反映一个数据集的离散程度，标准偏差越小，这些值偏离平均值就越少，反之亦然。其公式如下：

通过去除部分偏差较大的值后，对相关数据分析得到，测量距离为100 cm时，距离感知阈值的平均值为 7.62 cm，其中zui小值为1 cm，zui大值为14.4 cm，标准偏差为3.98 cm。测量距离为200 cm时，距离感知阈值的平均值为15.76cm，其中zui小值5.4 cm，zui大值28.2 cm，标准偏差为6.0 cm。

3 总结

本实验设计了三维音频感知敏感度的实验，使用高斯白噪声作为声源，通过改变水平角和距离，测量了水平方向0～180°，距离50～465 cm内136个测量点的DPS。根据实验数据，分析了距离、角度对距离感知敏感度的影响规律。相较于角度等其他因素，距离为影响DPS的主要因素；50～160 cm时，DPS的变化较小，160～465 cm时，DPS的变化较大；人对声源距离变化的感知在人耳的左右两侧更为明显；得到了不同距离时的距离感知阈值。在后续工作中，将扩大实验测量的范围，加入高度角等因素，以及音量、混响等交叉因素的综合影响，继续完善三维音频感知敏感度的研究。